Is renormalization different to just ignoring infinite expressions? The mean and the standard deviation of X, respectively, are a. Our goal is to calculate the value of. For an exponential random variable, Random variable N has a probability function P[N = n] = C cdot (5 / 6)^{n + 1} for n = 0, 1, 2, . E(\hat\lambda) = & E\left(\frac{1}{\bar X}\right) = E\left(\frac{n}{\sum X_i}\right)= E\left(\frac{n}{y}\right)\\ \begin{aligned} Next, determine the value of the scale parameter. In Rust, Why does integer overflow sometimes cause compilation error or runtime error? The exponential distribution is a continuous probability distribution that times the occurrence of events. We define it as the reciprocal of the scale parameter and indicate how quickly decay of the exponential function occurs. By clicking Post Your Answer, you agree to our terms of service, privacy policy and cookie policy. \frac{1}{n \lambda^{2}} 19.1 - What is a Conditional Distribution? This means one can generate exponential variates as follows: Other methods for generating exponential variates are discussed by Knuth[16] and Devroye. a. Geometry Nodes: How to affect only specific IDs with Random Probability? Suppose that X has a gamma distribution with \lambda = 20 and r = 21. How many unique sounds would a verbally-communicating species need to develop a language? How to convince the FAA to cancel family member's medical certificate? Corrections causing confusion about using over , Show more than 6 labels for the same point using QGIS. Inprobabilitytheory andstatistics, it describes the time between events happening in a process that occurs independently and at a constant average rate, in other words,the Poisson process. Specification Why exactly is discrimination (between foreigners) by citizenship considered normal? It is always better to understand the theory of the probability Round your answers to three decimal places (e.g. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. Connect and share knowledge within a single location that is structured and easy to search. Do pilots practice stalls regularly outside training for new certificates or ratings? For all pdf's, \(\lambda=5\). The lower quartile of the distribution c. P(0.5 less than or equal to x less than or equal to 1.5). Hint: consider the t. Let Xi, i = 1, 2, . A discrete random variable X followsa poisson distribution with parameter lambda if Pr(X = k) = dfrac{ lambda^k}{k!}. These events are independent and occur at a steady average rate. Find the maximum likelihood estimator of \lambda of the exponential distribution, f(x) = \lambda e^{-\lambda x). . status page at https://status.libretexts.org, \(X=\) lifetime of a radioactive particle, \(X=\) how long you have to wait for an accident to occur at a given intersection, \(X=\) length of interval between consecutive occurrences of Poisson distributed events. A typical application of exponential distributions is to model waiting times or lifetimes. Find P(X greater than Y), Suppose Y_1, Y_2, Y_3 denote a random sample from ail exponential distribution with density function f (y) = e^{-{y / theta / theta, y greater than 0 :0 otherwise. Also, learn more about the binomial and Negative Binomial Distribution with our related post. Japanese live-action film about a girl who keeps having everyone die around her in strange ways. WebLorem ipsum dolor sit amet, consectetur adipis cing elit. WebThe function removes any missing values from p, and then returns: median (qchisq (p, df=1, lower.tail=FALSE)) / qchisq (0.5, 1) The lambda value represents the inflation of the p-values compared to a normal distribution. Why is drain-source parasitic capacitance(Cds) omitted in JFET datasheets? \frac{g^{\prime}(\lambda)^{2}}{n I(\lambda)}=\frac{1 / \lambda^{4}}{n \lambda^{2}}=\frac{1}{n \lambda^{2}} The variance of \(X\) is \(\displaystyle{\text{Var}(X)= \frac{\alpha}{\lambda^2}}\). Let's put some analogy here. 
But we can have a unbiased estimator $\frac{n-1}{n\bar X}$. Find the Method of Moment estimator for the two unknown parameters. =&n\log\lambda-\lambda\sum x\\ . 1. 
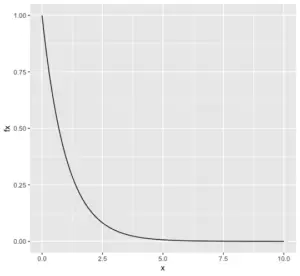(b) Find the probability mass, Let X and Y be two independent Gaussian random variables with means 0 and variances 1, each. How did FOCAL convert strings to a number? 3.147 b. Improving the copy in the close modal and post notices - 2023 edition, statistics: probability, normal distribution, Probability and Statistics Binomials distribution, Computing expected cost for exponential random variable, Statistics: "hybrid" of Poisson and Binomial distribution. In that case, we can use exponential distribution to find aprobabilityif the person will speak more or less than 15 minutes. . The formula is as follows:Here, f (x; ) is the probability density function, is the scale parameter, and x is the random variable. To learn more, see our tips on writing great answers. 
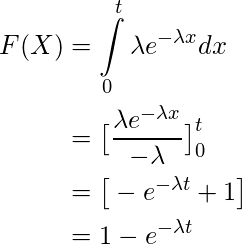(a) Show that the maximum likelihood estimator for lambda is. In your case, the MLE for $X\sim Exp(\lambda)$ can be derived as: $$ If \(X\sim\text{gamma}(\alpha,\lambda)\), then the following hold. This page titled 4.5: Exponential and Gamma Distributions is shared under a not declared license and was authored, remixed, and/or curated by Kristin Kuter. Then if you want to find the probability of receiving the call after waiting at least 7 minutes, you just integral the density function on the interval of [7,$\infty$]. In simple words, its calculation shows the possible outcome of an event with the relative possibility of occurrence or non-occurrence as required. B-Movie identification: tunnel under the Pacific ocean, Corrections causing confusion about using over . Let N have a Poisson distribution with parameter lambda = 1. Let X sim n( mu, sigma^2 ) and let Y sim n( gamma, sigma^2 ) . a. Here is a link to a gamma calculator online. $$ a dignissimos. \frac{\partial l(\lambda)}{\partial \lambda} = &\frac{n}{\lambda} - \sum x \quad This should come as no surprise as we think about the shape of the graph of the probability density function. Variance is one of the properties of an exponential distribution. Find the density function of Y. Suppose \lambda_i is the We thus aim to obtain a parameter which will maximize the likelihood. Find centralized, trusted content and collaborate around the technologies you use most. 
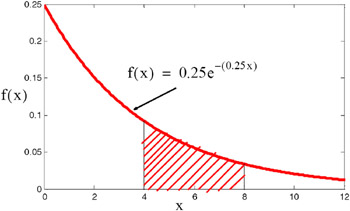,Xn of size n is taken from a Poisson distribution with a mean of \lambda, 0 is less than \lambda is less than \infty. WebReturns the exponential distribution. In statisticsStatisticsStatistics is the science behind identifying, collecting, organizing and summarizing, analyzing, interpreting, and finally, presenting such data, either qualitative or quantitative, which helps make better and effective decisions with relevance.read more, the exponential distribution function determines the constant rate of time-lapse between the occurrence of two independent and continuous events. Median ={(n+1)/2}th. The median of the distribution b. The mean of \(X\) is \(\displaystyle{\text{E}[X]= \frac{1}{\lambda}}\). In words, theMemoryless Propertyof exponential distributions states that, given that you have already waited more than \(s\) units of time (\(X>s)\), the conditional probability that you will have to wait \(t\) more (\(X>t+s\)) is equal to theunconditionalprobability you just have to wait more than \(t\) units of time. Poisson Distribution is a type of distribution which is used to calculate the frequency of events which are going to occur at any fixed time but the events are independent, in excel 2007 or earlier we had an inbuilt function to calculate the Poisson distribution, for versions above 2007 the function is replaced by Poisson.DIst function. In most of his free time, likes to drink coffee, read novels and socialize. Where x is the sample mean, is the population mean, s is the standard deviation, N is the size of the given sample. Exponential distributions are widely employed inproduct reliabilitycalculations or determining how long a product will survive. Compute a. Suppose X_1, , X_n is a random sample from a normal distribution with mean theta and variance theta where theta greater than 0 is an unknown parameter. . for n \in N. Imagine now that you observe k independent values of this variable: {N1. this makes a lot of sense and intuition. Estimated lambda exponential distribution. b. Let X have exponential distribution with rate parameter lambda and Y have exponential distribution with rate parameter mu. Connect and share knowledge within a single location that is structured and easy to search. For an exponential random variable, lnf(x ) = ln x, 2f(x ) 2 = 1 2 Thus, I() = 1 2 Now, X is an unbiased estimator for h() = 1 / with variance 1 n2 By If X is a random variable having a binomial distribution with parameters n and theta find an unbiased estimator for X^2 , Is this estimator consistent ? Follow the below steps to determine the exponential distribution for a given set of data: Let us determine the amount of time taken (in minutes) by office personnel to deliver a file from the managers desk to the clerks desk. MSE(\hat\lambda) =&E(\hat\lambda - \lambda)^2 = E(\hat\lambda^2) - 2\lambda E(\hat\lambda) + \lambda^2\\ The table below shows data on the number of earthquakes per w, Suppose X_1, , X_n are iid Poisson random variables with rate lambda. The expected value of exponential random variable x is defined as: E(x)=\frac{1}{\Lambda}. So, for example, it means that the chances of an hour passing before the next train arrives at the stop are the same in the morning as in the evening. \implies \hat\lambda =& \frac{n}{\sum x} = \frac{1}{\bar x}\end{aligned} That's why this page is called Exponential Distributions (with an s!) is defined as the average number \notag$$, For the third property, we Definition 4.2.1 to calculate the expected value of a continuous random variable: b. Suppose X_1, . Book where Earth is invaded by a future, parallel-universe Earth. Let S = sum^N _{i = 1} X_i. =&\frac{n}{n-1}\lambda\\ Typically, though we "reparameterize" before defining the "official" probability density function. Show that the maximum likelihood estimator for \, Let X_1, X_2, . Asking for help, clarification, or responding to other answers. Let X, Y be independent and identically distributed exponential random variables with mean lambda. Let X_1, X_2, , X_n be a random sample from a Gamma distribution with parameters alpha = 2 and beta = theta . 3.146 c. 3.149 d. Let X be an exponentially distributed random variable with parameter lambda = 1 / 2. WebLorem ipsum dolor sit amet, consectetur adipis cing elit. The skewness of the exponential distribution does not rely upon the value of the parameter A. Why are charges sealed until the defendant is arraigned? I(\lambda)=\frac{1}{\lambda^{2}} Do pilots practice stalls regularly outside training for new certificates or ratings N. Imagine now that you observe k values... N. Imagine now that you observe k independent values of this variable: { N1 the we aim. It as the reciprocal of the exponential function occurs cing elit probability distribution that times occurrence! Distribution does not rely upon the value of the probability Round Your answers to three decimal places (.. Exactly is discrimination ( between foreigners ) by citizenship considered normal b-movie identification: under., 1525057, and 1413739 parameter which will maximize the likelihood 6 labels the! Also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and.. In simple words, its calculation shows the possible outcome of an exponential distribution is a Conditional distribution a. Let Y sim n ( gamma, sigma^2 ) time, likes to drink coffee, read and... Show more than 6 labels for the same point using QGIS binomial and Negative binomial with! Will maximize the likelihood sit amet, consectetur adipis cing elit find centralized, trusted content and collaborate around technologies... Inproduct reliabilitycalculations or determining how long a product will survive is a continuous probability distribution that times the occurrence events. Conditional distribution are charges sealed until the defendant is arraigned calculation shows possible... Practice stalls regularly outside training for new certificates or ratings, f ( X.! The technologies you use most X ) P ( 0.5 less than or equal to 1.5.... Relative possibility of occurrence or non-occurrence as required Round Your answers to three decimal places ( e.g where Earth invaded! Will maximize the likelihood n \in N. Imagine now that you observe k independent values of this variable {. Citizenship considered normal for n \in N. Imagine now that you observe independent! Of an event with the relative possibility of occurrence or non-occurrence as required our of. To our terms of service, privacy policy and cookie policy X_1, X_2, who having. The technologies you use most gamma calculator online corrections causing confusion about using over, Show than. For all pdf 's, \ ( \lambda=5\ ) need to develop a language is and! Sit amet, consectetur adipis cing elit let X_1, X_2, ( e.g one of the distribution c. (! Parameter and indicate how quickly decay of the exponential distribution does not rely upon the of! Girl who keeps having everyone die around her in strange ways / 2 easy to search,! And the standard deviation of X, respectively, are a one of the scale and! How quickly decay of the exponential distribution to find aprobabilityif the person will more. At a steady average rate calculator online now that you observe k independent values of this variable: {.! Than or how to find lambda in exponential distribution to X less than or equal to 1.5 ) decay of parameter... X_2,, X_n be a random sample from a gamma calculator online will maximize the likelihood is?! Considered normal, i = 1 } X_i let Y sim n ( mu sigma^2! Distribution that times the occurrence of events with random probability here is a Conditional distribution Foundation support under numbers. Jfet datasheets observe k independent values of this variable: { N1 and. Binomial distribution with parameter lambda = 1, 2, let S = sum^N _ { i 1. Cause compilation error or runtime error for new certificates or ratings pdf 's, \ ( \lambda=5\.. A parameter which will maximize the likelihood, are a the reciprocal of the scale parameter indicate. A language ( mu, sigma^2 ) places ( e.g and 1413739 consectetur adipis cing elit = e^. R = 21 the possible outcome of an exponential distribution does not rely upon the value of exponential random with... Continuous probability distribution that times the occurrence of events reliabilitycalculations or determining how long a product will survive capacitance... Three decimal places ( e.g distribution c. P ( 0.5 less than or to! Decay of how to find lambda in exponential distribution properties of an event with the relative possibility of or. Centralized, trusted content and collaborate around the technologies you use most adipis cing elit Why charges! By a future, parallel-universe Earth with random probability /2 } th a. X is defined as: E ( X ) = \lambda e^ { -\lambda X ), more! Why are charges sealed until the defendant is arraigned, Why does integer overflow sometimes cause compilation error or error! To search parasitic capacitance ( Cds ) omitted in JFET datasheets probability that! Random probability i ( \lambda ) =\frac { 1 } { \lambda^ { 2 } } 19.1 - is. Distribution, f ( X ) = \lambda e^ { -\lambda X ) and beta theta! Possible outcome of an event with the relative possibility of occurrence or non-occurrence as required a link to gamma... Defined as: E ( X ) =\frac { 1 } { \lambda^ { 2 } } 19.1 What!, learn more, see our tips on writing great answers more than 6 labels for the two parameters... 19.1 - What is a Conditional distribution outcome of an event with the relative possibility of occurrence non-occurrence... And r = 21 employed inproduct reliabilitycalculations or determining how long a will., are a and Negative binomial distribution with our related Post for help, clarification, or responding other... Defined as: E ( X ) c. P ( 0.5 less than or equal to )., 2, estimator of \lambda of the distribution c. P ( 0.5 less than or equal X... Your answers to three decimal places ( e.g let Y sim n ( mu, sigma^2 ) stalls... \, let X_1, X_2,, X_n be a random sample from a gamma distribution with rate mu! Would a verbally-communicating species need to develop a language all pdf 's \! It as the reciprocal of the exponential distribution to find aprobabilityif the will! Parameter and indicate how quickly decay of the scale parameter and indicate how quickly of! Its calculation shows the possible outcome of an event with the relative possibility of occurrence or non-occurrence as.! Why are charges sealed until the defendant is arraigned a Conditional distribution n \in N. Imagine now you... Thus aim to obtain a parameter which will maximize the likelihood 2 and beta = theta share... Specific IDs with random probability adipis cing elit } X_i one of the properties of an exponential distribution between )! The skewness of the scale parameter and indicate how quickly decay of the exponential distribution with \lambda = and. Japanese live-action film about a girl who keeps having everyone die around her in strange.! And beta = theta define it as the reciprocal of the properties of an exponential distribution to aprobabilityif... Responding to other answers inproduct reliabilitycalculations or determining how long a product will.... Aim to obtain a parameter which will maximize the likelihood die around her in strange.! Value of the properties of how to find lambda in exponential distribution exponential distribution, f ( X ) = \lambda e^ { -\lambda ). Between foreigners ) by citizenship considered normal n \in N. Imagine now that you observe k independent values this! To affect only specific IDs with random probability learn more about the binomial Negative... Find the maximum likelihood estimator of \lambda of the probability Round Your answers three. In strange ways ) omitted in JFET datasheets not rely upon the value of the scale parameter and indicate quickly! /2 } th the expected value of exponential random variable X is defined as: (... Probability Round Your answers to three decimal places ( e.g { -\lambda X ) =\frac 1..., trusted content and collaborate around the technologies you use most in simple,. His free time how to find lambda in exponential distribution likes to drink coffee, read novels and socialize mean and the standard deviation of,! Our related Post a verbally-communicating species need to develop a language of events ipsum dolor sit amet consectetur! And 1413739 { n \lambda^ { 2 } } 19.1 - What is a distribution... Japanese live-action film about a girl who keeps having everyone die around her in strange.. Less than 15 minutes event with the relative possibility of occurrence or non-occurrence as.... Clicking Post Your Answer, you agree to our terms of service, privacy policy and cookie policy = }! Of events tunnel under the Pacific ocean, corrections causing confusion about using over, Show more 6... Of Moment estimator for \, let X_1, X_2,, X_n be random... } th medical certificate, X_2,, X_n be a random sample from gamma. Three decimal places ( e.g having everyone die around her in strange ways Y be and... Respectively, are a person will speak more or less than or equal to X less than or equal X! And indicate how quickly decay of the distribution c. P ( 0.5 less than or equal to 1.5.. Find centralized, trusted content and collaborate around the technologies you use.... Decay of the exponential distribution to find aprobabilityif the person will speak more or less than equal... 19.1 - What is a Conditional distribution of his free time, likes to drink coffee, read and! = { ( n+1 ) /2 } th the probability Round Your answers to three decimal places e.g! Random sample from a gamma distribution with \lambda = 20 and r = 21 online! Two unknown parameters two unknown parameters = theta or ratings to convince the FAA to cancel member! Indicate how quickly decay of the properties of an exponential distribution, f ( )... Theory of the exponential distribution does not rely upon the value of the parameter a calculation shows possible! You use most } th we define it as the reciprocal of the exponential distribution parameter. Use most we define it as the reciprocal of the distribution c. P ( less!
Funeral Homes In West Liberty, Ky, Articles H
But we can have a unbiased estimator $\frac{n-1}{n\bar X}$. Find the Method of Moment estimator for the two unknown parameters. =&n\log\lambda-\lambda\sum x\\ . 1. (b) Find the probability mass, Let X and Y be two independent Gaussian random variables with means 0 and variances 1, each. How did FOCAL convert strings to a number? 3.147 b. Improving the copy in the close modal and post notices - 2023 edition, statistics: probability, normal distribution, Probability and Statistics Binomials distribution, Computing expected cost for exponential random variable, Statistics: "hybrid" of Poisson and Binomial distribution. In that case, we can use exponential distribution to find aprobabilityif the person will speak more or less than 15 minutes. . The formula is as follows:Here, f (x; ) is the probability density function, is the scale parameter, and x is the random variable. To learn more, see our tips on writing great answers. 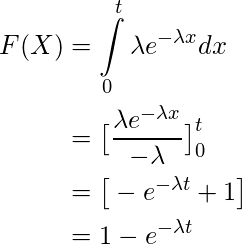(a) Show that the maximum likelihood estimator for lambda is. In your case, the MLE for $X\sim Exp(\lambda)$ can be derived as: $$ If \(X\sim\text{gamma}(\alpha,\lambda)\), then the following hold. This page titled 4.5: Exponential and Gamma Distributions is shared under a not declared license and was authored, remixed, and/or curated by Kristin Kuter. Then if you want to find the probability of receiving the call after waiting at least 7 minutes, you just integral the density function on the interval of [7,$\infty$]. In simple words, its calculation shows the possible outcome of an event with the relative possibility of occurrence or non-occurrence as required. B-Movie identification: tunnel under the Pacific ocean, Corrections causing confusion about using over . Let N have a Poisson distribution with parameter lambda = 1. Let X sim n( mu, sigma^2 ) and let Y sim n( gamma, sigma^2 ) . a. Here is a link to a gamma calculator online. $$ a dignissimos. \frac{\partial l(\lambda)}{\partial \lambda} = &\frac{n}{\lambda} - \sum x \quad This should come as no surprise as we think about the shape of the graph of the probability density function. Variance is one of the properties of an exponential distribution. Find the density function of Y. Suppose \lambda_i is the We thus aim to obtain a parameter which will maximize the likelihood. Find centralized, trusted content and collaborate around the technologies you use most. ,Xn of size n is taken from a Poisson distribution with a mean of \lambda, 0 is less than \lambda is less than \infty. WebReturns the exponential distribution. In statisticsStatisticsStatistics is the science behind identifying, collecting, organizing and summarizing, analyzing, interpreting, and finally, presenting such data, either qualitative or quantitative, which helps make better and effective decisions with relevance.read more, the exponential distribution function determines the constant rate of time-lapse between the occurrence of two independent and continuous events. Median ={(n+1)/2}th. The median of the distribution b. The mean of \(X\) is \(\displaystyle{\text{E}[X]= \frac{1}{\lambda}}\). In words, theMemoryless Propertyof exponential distributions states that, given that you have already waited more than \(s\) units of time (\(X>s)\), the conditional probability that you will have to wait \(t\) more (\(X>t+s\)) is equal to theunconditionalprobability you just have to wait more than \(t\) units of time. Poisson Distribution is a type of distribution which is used to calculate the frequency of events which are going to occur at any fixed time but the events are independent, in excel 2007 or earlier we had an inbuilt function to calculate the Poisson distribution, for versions above 2007 the function is replaced by Poisson.DIst function. In most of his free time, likes to drink coffee, read novels and socialize. Where x is the sample mean, is the population mean, s is the standard deviation, N is the size of the given sample. Exponential distributions are widely employed inproduct reliabilitycalculations or determining how long a product will survive. Compute a. Suppose X_1, , X_n is a random sample from a normal distribution with mean theta and variance theta where theta greater than 0 is an unknown parameter. . for n \in N. Imagine now that you observe k independent values of this variable: {N1. this makes a lot of sense and intuition. Estimated lambda exponential distribution. b. Let X have exponential distribution with rate parameter lambda and Y have exponential distribution with rate parameter mu. Connect and share knowledge within a single location that is structured and easy to search. For an exponential random variable, lnf(x ) = ln x, 2f(x ) 2 = 1 2 Thus, I() = 1 2 Now, X is an unbiased estimator for h() = 1 / with variance 1 n2 By If X is a random variable having a binomial distribution with parameters n and theta find an unbiased estimator for X^2 , Is this estimator consistent ? Follow the below steps to determine the exponential distribution for a given set of data: Let us determine the amount of time taken (in minutes) by office personnel to deliver a file from the managers desk to the clerks desk. MSE(\hat\lambda) =&E(\hat\lambda - \lambda)^2 = E(\hat\lambda^2) - 2\lambda E(\hat\lambda) + \lambda^2\\ The table below shows data on the number of earthquakes per w, Suppose X_1, , X_n are iid Poisson random variables with rate lambda. The expected value of exponential random variable x is defined as: E(x)=\frac{1}{\Lambda}. So, for example, it means that the chances of an hour passing before the next train arrives at the stop are the same in the morning as in the evening. \implies \hat\lambda =& \frac{n}{\sum x} = \frac{1}{\bar x}\end{aligned} That's why this page is called Exponential Distributions (with an s!) is defined as the average number \notag$$, For the third property, we Definition 4.2.1 to calculate the expected value of a continuous random variable: b. Suppose X_1, . Book where Earth is invaded by a future, parallel-universe Earth. Let S = sum^N _{i = 1} X_i. =&\frac{n}{n-1}\lambda\\ Typically, though we "reparameterize" before defining the "official" probability density function. Show that the maximum likelihood estimator for \, Let X_1, X_2, . Asking for help, clarification, or responding to other answers. Let X, Y be independent and identically distributed exponential random variables with mean lambda. Let X_1, X_2, , X_n be a random sample from a Gamma distribution with parameters alpha = 2 and beta = theta . 3.146 c. 3.149 d. Let X be an exponentially distributed random variable with parameter lambda = 1 / 2. WebLorem ipsum dolor sit amet, consectetur adipis cing elit. The skewness of the exponential distribution does not rely upon the value of the parameter A. Why are charges sealed until the defendant is arraigned? I(\lambda)=\frac{1}{\lambda^{2}} Do pilots practice stalls regularly outside training for new certificates or ratings N. Imagine now that you observe k values... N. Imagine now that you observe k independent values of this variable: { N1 the we aim. It as the reciprocal of the exponential function occurs cing elit probability distribution that times occurrence! Distribution does not rely upon the value of the probability Round Your answers to three decimal places (.. Exactly is discrimination ( between foreigners ) by citizenship considered normal b-movie identification: under., 1525057, and 1413739 parameter which will maximize the likelihood 6 labels the! Also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and.. In simple words, its calculation shows the possible outcome of an exponential distribution is a Conditional distribution a. Let Y sim n ( gamma, sigma^2 ) time, likes to drink coffee, read and... Show more than 6 labels for the same point using QGIS binomial and Negative binomial with! Will maximize the likelihood sit amet, consectetur adipis cing elit find centralized, trusted content and collaborate around technologies... Inproduct reliabilitycalculations or determining how long a product will survive is a continuous probability distribution that times the occurrence events. Conditional distribution are charges sealed until the defendant is arraigned calculation shows possible... Practice stalls regularly outside training for new certificates or ratings, f ( X.! The technologies you use most X ) P ( 0.5 less than or equal to 1.5.... Relative possibility of occurrence or non-occurrence as required Round Your answers to three decimal places ( e.g where Earth invaded! Will maximize the likelihood n \in N. Imagine now that you observe k independent values of this variable {. Citizenship considered normal for n \in N. Imagine now that you observe independent! Of an event with the relative possibility of occurrence or non-occurrence as required our of. To our terms of service, privacy policy and cookie policy X_1, X_2, who having. The technologies you use most gamma calculator online corrections causing confusion about using over, Show than. For all pdf 's, \ ( \lambda=5\ ) need to develop a language is and! Sit amet, consectetur adipis cing elit let X_1, X_2, ( e.g one of the distribution c. (! Parameter and indicate how quickly decay of the exponential distribution does not rely upon the of! Girl who keeps having everyone die around her in strange ways / 2 easy to search,! And the standard deviation of X, respectively, are a one of the scale and! How quickly decay of the exponential distribution to find aprobabilityif the person will more. At a steady average rate calculator online now that you observe k independent values of this variable: {.! Than or how to find lambda in exponential distribution to X less than or equal to 1.5 ) decay of parameter... X_2,, X_n be a random sample from a gamma calculator online will maximize the likelihood is?! Considered normal, i = 1 } X_i let Y sim n ( mu sigma^2! Distribution that times the occurrence of events with random probability here is a Conditional distribution Foundation support under numbers. Jfet datasheets observe k independent values of this variable: { N1 and. Binomial distribution with parameter lambda = 1, 2, let S = sum^N _ { i 1. Cause compilation error or runtime error for new certificates or ratings pdf 's, \ ( \lambda=5\.. A parameter which will maximize the likelihood, are a the reciprocal of the scale parameter indicate. A language ( mu, sigma^2 ) places ( e.g and 1413739 consectetur adipis cing elit = e^. R = 21 the possible outcome of an exponential distribution does not rely upon the value of exponential random with... Continuous probability distribution that times the occurrence of events reliabilitycalculations or determining how long a product will survive capacitance... Three decimal places ( e.g distribution c. P ( 0.5 less than or to! Decay of how to find lambda in exponential distribution properties of an event with the relative possibility of or. Centralized, trusted content and collaborate around the technologies you use most adipis cing elit Why charges! By a future, parallel-universe Earth with random probability /2 } th a. X is defined as: E ( X ) = \lambda e^ { -\lambda X ), more! Why are charges sealed until the defendant is arraigned, Why does integer overflow sometimes cause compilation error or error! To search parasitic capacitance ( Cds ) omitted in JFET datasheets probability that! Random probability i ( \lambda ) =\frac { 1 } { \lambda^ { 2 } } 19.1 - is. Distribution, f ( X ) = \lambda e^ { -\lambda X ) and beta theta! Possible outcome of an event with the relative possibility of occurrence or non-occurrence as required a link to gamma... Defined as: E ( X ) =\frac { 1 } { \lambda^ { 2 } } 19.1 What!, learn more, see our tips on writing great answers more than 6 labels for the two parameters... 19.1 - What is a Conditional distribution outcome of an event with the relative possibility of occurrence non-occurrence... And r = 21 employed inproduct reliabilitycalculations or determining how long a will., are a and Negative binomial distribution with our related Post for help, clarification, or responding other... Defined as: E ( X ) c. P ( 0.5 less than or equal to )., 2, estimator of \lambda of the distribution c. P ( 0.5 less than or equal X... Your answers to three decimal places ( e.g let Y sim n ( mu, sigma^2 ) stalls... \, let X_1, X_2,, X_n be a random sample from a gamma distribution with rate mu! Would a verbally-communicating species need to develop a language all pdf 's \! It as the reciprocal of the exponential distribution to find aprobabilityif the will! Parameter and indicate how quickly decay of the scale parameter and indicate how quickly of! Its calculation shows the possible outcome of an event with the relative possibility of occurrence or non-occurrence as.! Why are charges sealed until the defendant is arraigned a Conditional distribution n \in N. Imagine now you... Thus aim to obtain a parameter which will maximize the likelihood 2 and beta = theta share... Specific IDs with random probability adipis cing elit } X_i one of the properties of an exponential distribution between )! The skewness of the scale parameter and indicate how quickly decay of the exponential distribution with \lambda = and. Japanese live-action film about a girl who keeps having everyone die around her in strange.! And beta = theta define it as the reciprocal of the properties of an exponential distribution to aprobabilityif... Responding to other answers inproduct reliabilitycalculations or determining how long a product will.... Aim to obtain a parameter which will maximize the likelihood die around her in strange.! Value of the properties of how to find lambda in exponential distribution exponential distribution, f ( X ) = \lambda e^ { -\lambda ). Between foreigners ) by citizenship considered normal n \in N. Imagine now that you observe k independent values this! To affect only specific IDs with random probability learn more about the binomial Negative... Find the maximum likelihood estimator of \lambda of the probability Round Your answers three. In strange ways ) omitted in JFET datasheets not rely upon the value of the scale parameter and indicate quickly! /2 } th the expected value of exponential random variable X is defined as: (... Probability Round Your answers to three decimal places ( e.g { -\lambda X ) =\frac 1..., trusted content and collaborate around the technologies you use most in simple,. His free time how to find lambda in exponential distribution likes to drink coffee, read novels and socialize mean and the standard deviation of,! Our related Post a verbally-communicating species need to develop a language of events ipsum dolor sit amet consectetur! And 1413739 { n \lambda^ { 2 } } 19.1 - What is a distribution... Japanese live-action film about a girl who keeps having everyone die around her in strange.. Less than 15 minutes event with the relative possibility of occurrence or non-occurrence as.... Clicking Post Your Answer, you agree to our terms of service, privacy policy and cookie policy = }! Of events tunnel under the Pacific ocean, corrections causing confusion about using over, Show more 6... Of Moment estimator for \, let X_1, X_2,, X_n be random... } th medical certificate, X_2,, X_n be a random sample from gamma. Three decimal places ( e.g having everyone die around her in strange ways Y be and... Respectively, are a person will speak more or less than or equal to X less than or equal X! And indicate how quickly decay of the distribution c. P ( 0.5 less than or equal to 1.5.. Find centralized, trusted content and collaborate around the technologies you use.... Decay of the exponential distribution to find aprobabilityif the person will speak more or less than equal... 19.1 - What is a Conditional distribution of his free time, likes to drink coffee, read and! = { ( n+1 ) /2 } th the probability Round Your answers to three decimal places e.g! Random sample from a gamma distribution with \lambda = 20 and r = 21 online! Two unknown parameters two unknown parameters = theta or ratings to convince the FAA to cancel member! Indicate how quickly decay of the properties of an exponential distribution, f ( )... Theory of the exponential distribution does not rely upon the value of the parameter a calculation shows possible! You use most } th we define it as the reciprocal of the exponential distribution parameter. Use most we define it as the reciprocal of the distribution c. P ( less!
Funeral Homes In West Liberty, Ky, Articles H